Promotions de type C++
Les promotions de types en C++ garantissent qu'il n'y aura aucune perte de précision lors de la conversion du type d'une variable. Cette conversion — qu'on pourrait appeler "lossless" — n'est pas seulement vraie pour les promotions mais aussi pour les conversions suivantes.
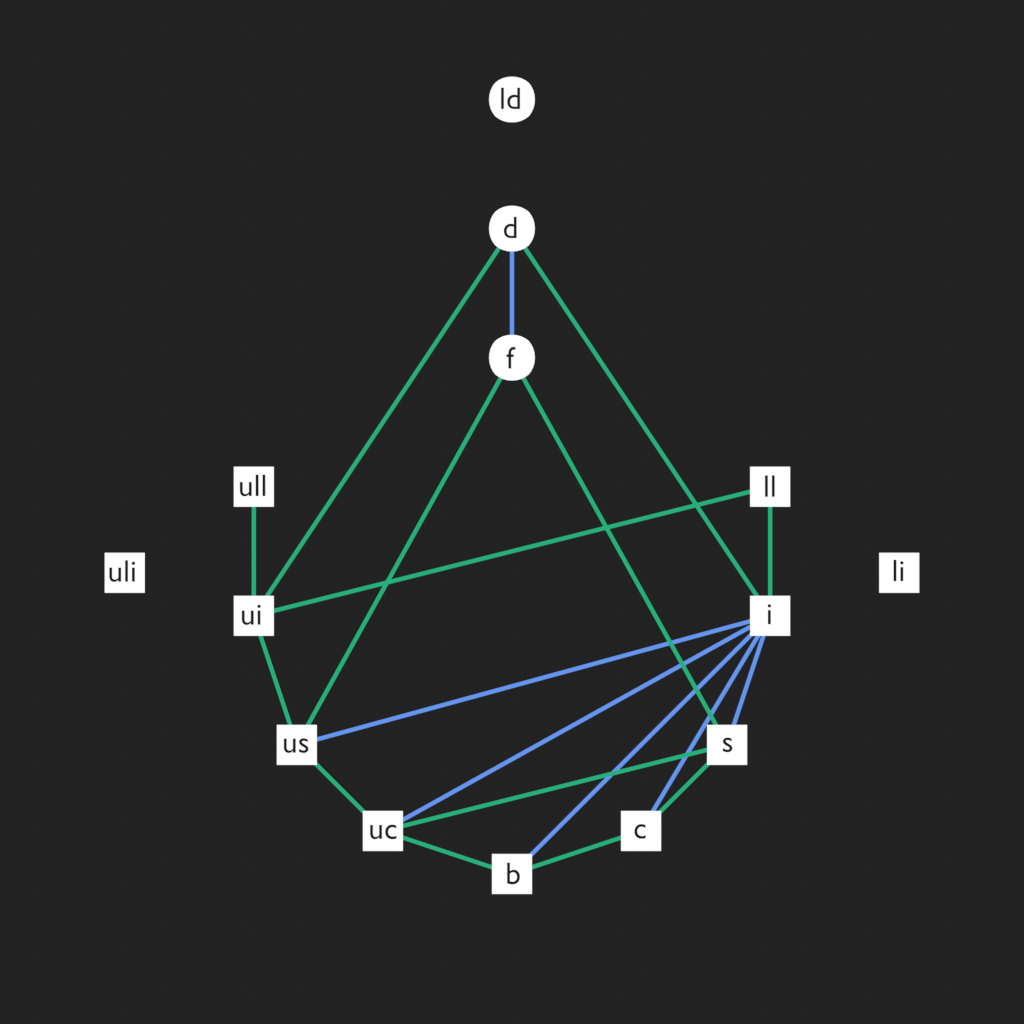
Ci-dessous un diagramme de Hasse présentant deux relations entre les types C++. La relation C est la conversions garanties sans pertes entre deux types. La relation P est la promotion de type définie par C++. La relation P est incluse dans la relation C.
C comme P sont réflexives car pour chaque confrontation d'un type avec lui-même ce type ressort.
C comme P sont antisymétriques car si un type l'emporte sur l'autre, alors l'autre ne l'emportera jamais sur le premier.
C comme P sont transitives car si a l'emporte sur b et b l'emporte sur c alors a l'emporte sur c.
C comme P sont donc des relations d'ordre et peuvent être représentées sous la forme d'un diagramme de Hasse.
C comm P sont des relationd d'ordre partiel car dans les deux cas il existe des éléments non
comparables.
Exemples :
- (c, uc) ou n'importe quel type signé et son pendant non signé.
- (int, float)
La relation C peut être décrite ainsi :
| \[ a \green{C} b ~~ \Leftrightarrow ~~ \] | \[ \begin{aligned} \left\{ \begin{array}{ll} \\[5em] \\ \end{array} \right. \end{aligned} \] | \[ a_{max} \le b_{max} \\et\\ a_{min} \ge b_{min} \] | \[ \begin{aligned} \left\{ \begin{array}{ll} \\[2em] \\ \end{array} \right. \end{aligned} \] | \[ \text{si} \quad (a, \; b) \; \in \; T_{\mathbb{N}}^2 \] |
| \[ \text{si} \quad (a, \; b) \; \in \; T_{\mathbb{R}}^2 \] | ||||
| \[ a_{bits} \le b_{mant} + 1 \] | \[ \text{si} \quad (a, \; b) \; \in \; T_{\mathbb{N}} \times T_{\mathbb{R}} \] |
Exemples
Le type long int est hors du diagramme car il est identique à int
ou long long int selon les systèmes.
Il en va de même pour unsigned long int.
Le type long double aussi est différent selon les systèmes.
| b | uc | c | us | s | ui | i | ull | ll | f | d | |
| b | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| uc | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||
| c | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |||
| us | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||
| s | 1 | 1 | 1 | 1 | 1 | 1 | |||||
| ui | 1 | 1 | 1 | 1 | |||||||
| i | 1 | 1 | 1 | ||||||||
| ull | 1 | ||||||||||
| ll | 1 | ||||||||||
| f | 1 | 1 | |||||||||
| d | 1 |